BOJ) 구간 합 구하기 (2042 번)

구간 합 구하기

2042번: 구간 합 구하기

 

세그먼트 트리를 이용해서 푸는 문제다.

우선, 이 문제를 풀기 위해서 세그먼트 트리에 대해서 공부해야했다.

백준 사이트에 블로그란에 기재되어있는 세그먼트 트리를 보고 풀었다.

 

 

세그먼트 트리란 무엇인가??

먼저, 세그먼트 트리는 배열의 크기가 커질 경우, 연산 식에 유용하다.

공간 복잡도가 O(N^2)이고 시간 복잡도가 O(N^2)인 배열에 대한 연산이 있다면, 세그먼트 트리를 이용하여 O(N log N)의 공간 복잡도를 갖게하고, O(log N)의 시간 복잡도를 갖게할 수 있다.

 

 

 

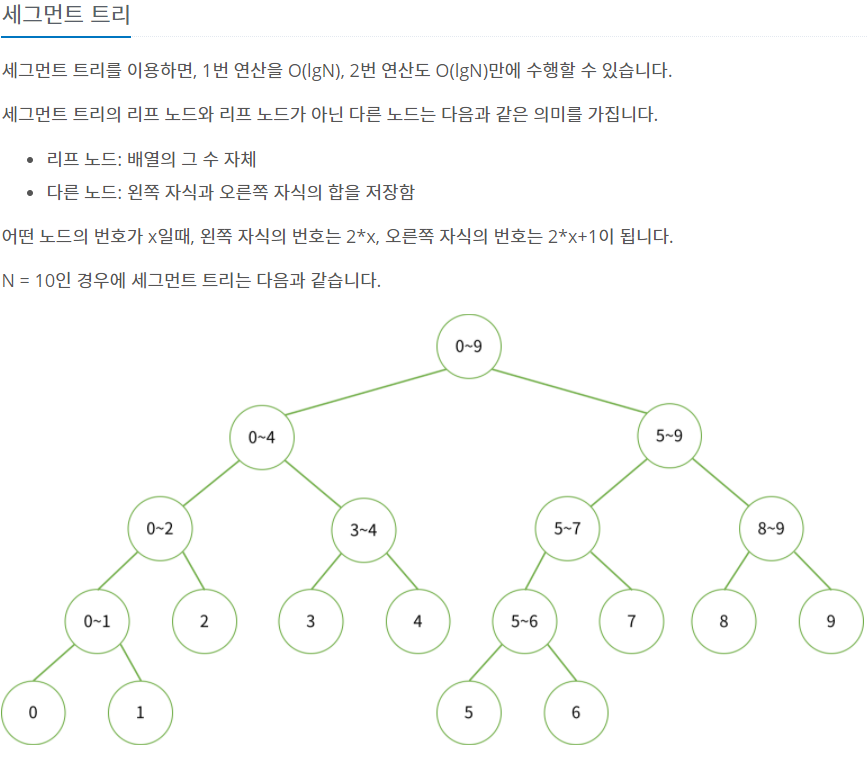
위의 그림처럼 리프 노드에는 주어진 배열의 수를 입력하고, 리프 노드가 아닌 노드에는 연산의 결과 값을 저장한다.

이 문제에서는 주어진 a ~ b에 대해 구간의 합을 출력하기 때문에, 인덱스 범위에 있는 값들의 합을 저장해준다.

 

위의 그림에서 보듯, 세그먼트 트리를 만드는데 필요한 배열의 크기는 2^(H+1) -1가 된다.

H = log2 N이 된다. 즉, N이 2의 제곱인 경우는 Full Binary Tree가 되어 2*N -1개가 된다.

다른 블로그 글을 찾아보면서, 위의 수식을 구하기 귀찮으면 4*N으로 사이즈를 정해도 된다고는 한다.

하지만, 공간이 남는 경우가 생기기 때문에 가급적 배열의 크기를 구하는 법은 익히는게 좋다고 판단했다.

(이 코드에서는 귀찮아서 4*N으로 쓰기는 했다.. )

 

세그먼트 트리 초기화

 

 

start == end 경우, node가 리프 노드인 경우라고 한다. 즉, 배열의 값을 그대로 대입해준다. ( tree[node] = a[start] )

위의 그림에서 알 수 있듯, node 의 왼쪽 자식은 node*2, 오른쪽 자식은 node*2+1이 된다.

따라서, node가 담당하는 구간이 [start,end] 라면

왼쪽 자식은 [start,(start+end)/2]를

오른쪽 자식은 [(start+end)/2+1,end]를 담당해야 한다.

재귀 함수를 이용해서 왼쪽 자식과 오른쪽 자식 트리를 만들고, 범위의 합을 저장해준다.

 

구간 합 찾기

 

 

 

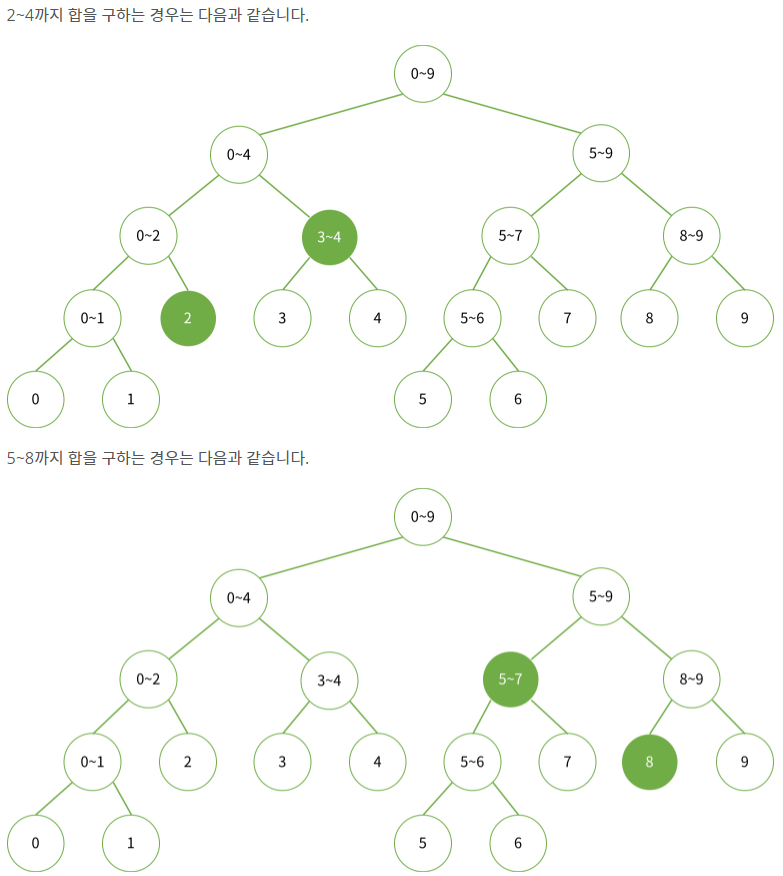
node가 담당하고 있는 구간이 [start,end] 이고, 합을 구해야하는 구간이 [left,right] 이라면 4가지 경우로 나뉜다.

 

1) [left,right]와 [start,end]가 겹치지 않는 경우 ( 담당하는 구간이 다른 경우 ~> out of range)

2) [left,right]가 [start,end]를 완전히 포함하는 경우( 리프 노드가 node가 담당하는 구간 상위에 있는 경우 )

3) [start,end]가 [left,right]를 완전히 포함하는 경우 ( 리프 노드보다 담당하는 구간이 더 큰 경우 )

4) [left,right]와 [start,end]가 겹쳐져 있는 경우 (1, 2, 3 제외한 나머지 경우)

 

1번)

if (left > end || right < start) 로 나타낼 수 있다.

이 경우에는 구간이 겹치지 않기 때문에, 탐색을 이어나갈 필요가 없다.

 

2번)

if (left <= start && end <= right)로 나타낼 수 있다.

구해야하는 합의 범위는 [left,right]인데, [start,end]는 그 범위에 모두 포함되고, 그 node의 자식도 모두 포함되기 때문에 계속 호출을 하는 것은 비효율적이다.

 

3번 & 4번)

왼쪽 자식과 오른쪽 자식을 루트로 하는 트리에서 다시 탐색을 해야한다.

 

노드 번호를 각각 왼쪽 자식과 오른쪽 자식으로 탐색해서 합을 반환해준다.

 

업데이트

 

 

 

 

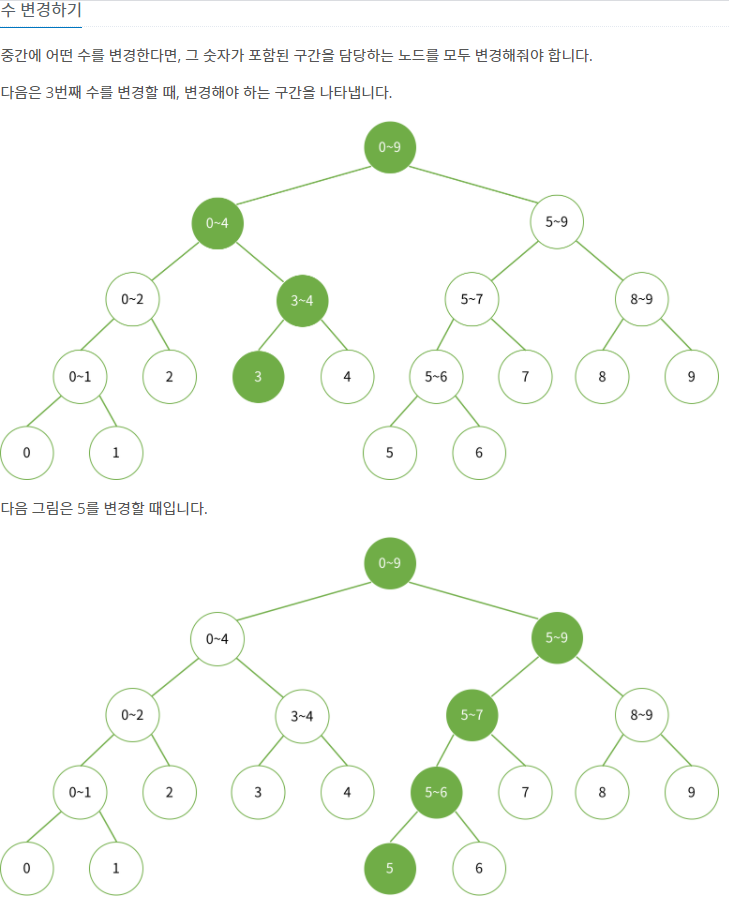
index번째를 특정 값으로 변경한다면, 그 수가 얼마만큼 변했는지를 알아야 한다.

이 수를 diff라고 하면, diff = val - a[index] 로 변한 값을 구해준다.

 

수 변경은 2가지 경우가 있다.

 

1) [start,end]에 index가 포함되는 경우

2) [start,end]에 index가 포함되지 않는 경우

 

node의 구간에 포함되는 경우에는 diff만큼 증가시켜 합을 변경해 준다.

tree[node] = tree[node] + diff 에 포함되지 않는 경우, 그 자식의 범위도 index가 포함되지 않으므로, 탐색을 중단한다.

 

리프 노드가 아닌 경우에는 자식도 변경해줘야 하기 때문에, start != end로 리프 노드인지 검사해야 한다.

(리프 노드가 아니라면, 배열에서 저장한 값을 그대로 가지고 있기 때문에)

 

이 문제는 펜윅 트리로도 풀 수 있다고 백준 블로그에 적혀있다.

펜윅 트리에 대한 내용은 학습한 이후 업데이트 하도록 해야겠다.

 

코드

 

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class IntervalSum_2042 {
    final static int UPDATE =1, SUM =2;
    final static String NEWLINE = "\n";

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int n = Integer.parseInt(st.nextToken()), m = Integer.parseInt(st.nextToken()), k = Integer.parseInt(st.nextToken());
        long[] numArr = new long[n];
        for(int i=0; i<n; i++) {
            numArr[i] = Long.parseLong(br.readLine());
        }

        m+=k;
        long[][] commandArr = new long[m][3];
        for(int i=0; i<m; i++) {
            st = new StringTokenizer(br.readLine());
            for(int j=0; j<3; j++) {
                commandArr[i][j] = Long.parseLong(st.nextToken());
            }
        }
        br.close();
        solution(n, numArr, commandArr);
    }

    private static void solution(int n, long[] numArr, long[][] commandArr) {
        SegmentTree segmentTree = new SegmentTree(n, numArr);
        segmentTree.init(1, 0, n-1);
        StringBuilder sb = new StringBuilder();

        for(long[] commandInfos : commandArr) {
            final int command = (int) commandInfos[0];
            if(command == UPDATE) {
                int index = (int) commandInfos[1]-1;
                long diff = commandInfos[2] - numArr[index];
                numArr[index] = commandInfos[2];
                segmentTree.update(1, 0, n-1, index, diff);
            } else if(command == SUM) {
                int left = (int) commandInfos[1] -1, right = (int) commandInfos[2]-1;
                sb.append(segmentTree.sum(1, 0, n-1, left, right)).append(NEWLINE);
            }
        }
        System.out.println(sb.toString());
    }

    private static class SegmentTree {
        long[] tree, numArr;
        private int size;

        public SegmentTree(int n, long[] numArr) {
            this.size = 4*n;
            this.tree = new long[this.size];
            this.numArr = numArr;
        }

        public long init(int node, int start, int end) {
            if(start == end) {
                return this.tree[node] = this.numArr[start];
            }
            int mid = (start+end)/2;
            return tree[node] = this.init(node*2, start, mid) + this.init(node*2+1, mid+1, end);
        }

        public void update(int node, int start, int end, int index, long diff) {
            if (index < start || index > end){
                return;
            }
            tree[node] = tree[node] + diff;
            if (start != end) {
                int mid = (start+end)/2;
                this.update(node*2, start, mid, index, diff);
                this.update(node*2+1, mid+1, end, index, diff);
            }
        }

        public long sum(int node, int start, int end, int left, int right) {
            if(left > end || right < start) {
                return 0;
            }
            if(left <= start && right >= end) {
                return this.tree[node];
            }
            int mid = (start+end)/2;
            return this.sum(node*2, start, mid, left, right) + this.sum(node*2+1, mid +1, end, left, right);
        }
    }
}